1 背景知识
1.1 简介
实时的海面渲染是我最近一个星期在思考与试图解决的一个问题。不纯粹是理论上的,也是实际的项目需要。
在实现实时海面渲染的时候,最直接的想法就是将海面当做一个四边形的面,每帧动态改变其顶点,从而实现实时渲染。但这个方法在海面很大的时候,对计算机的性能要求很大,而且也很难做到真实。
相比于其他物体的渲染,海面渲染有这样一些与众不同的特征:
- 它是动态的。由于海面在每一帧的每一个点的高度都不一样,同时还会因为与其他物体接触而产生形变,所以计算每一帧的海面的高度是复杂的。
- 它的表面积很大。这个无需多言。
- 它的表面表现形式在很大程度上要依赖于光线的折射和反射效果。海面每一点的反射和折射比例在很大程度上取决于摄像机的位置。而且海面的折射和反射效果直接决定了海面的真实程度。
由于海面渲染是如此之复杂,所以很多游戏中对它进行了简化处理。如:减小海面的表面积,甚至将海面改为水池或水缸。如:简化海面的与其他的物体的交互,甚至根本没有交互。如:简化海面的波浪多少,甚至到海面根本没有波浪,仅仅只由shader实现波纹效果。
这一节的下面部分会大致介绍海面渲染是如何实现的。
1.2 渲染管线简介
blabla
1.3 高度图简介
blabla
1.4 LOD 简介
blabla
1.5 波浪生成简介
blabla
1.6 水面光学效果简介
blabla
2. 网格投影法的基本概念
2.1 渲染中的空间变换
这一节中的概念是我参考了《Unity Shader入门精要》[^footnote1]一书中第四章的内容。
在渲染流水线中,一个顶点要经历许多坐标空间变化才能被最终画在屏幕上。这个顶点首先在它自己的模型空间中,最终变换到屏幕上的像素点坐标上。
2.1.1 模型空间
模型空间以模型的中心为原点的坐标空间。
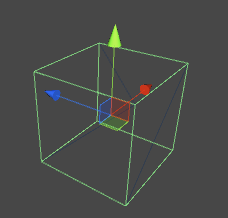
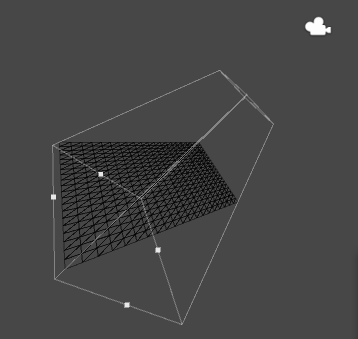
如上图这个正方体,其8个顶点在模型空间的坐标,就是相对正方体的中心(图中坐标轴的原点)的坐标。
2.1.2 世界空间
世界空间是我们最熟悉的空间,每个点在世界空间中的坐标可以直接通过查看Unity的Transfrom组件中的position来查看。

将物体从模型空间变换到世界空间的矩阵通常叫 $M_{model}$。其变化的公式为:
$$P_{world} = M_{model}P_{model}$$
其中 $P_{model}$ 为(列向量):
$$P_{model} = \begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix}
$$
2.1.3 观察空间(摄像机空间)
观察空间顾名思义,就是以观察者为原点的空间。在游戏中,它指的是以摄像机为原点,摄像机的前、右、上三个方向为坐标轴的空间。

需要注意的是,在Unity中,观察空间是右手坐标系,所以观察空间中,x+是摄像机的右方,y+是摄像机的上方,但z+是摄像机的后方。
如果已知摄像机的三个方向的方向向量在世界坐标系下的表示(可以根据 transfrom.up、tranform.right 和 transfrom.forward 得到),那么可以求出 将物体从世界空间到观察空间的矩阵 $M_{view}$:
假设观察空间坐标系方向向量在世界坐标系中分别为(单位向量): $\overrightarrow {Up}、\overrightarrow {Right}、\overrightarrow {Forward}$
摄像机在世界空间中的坐标为:$O_{origin}$则:
$$M_{view} = M_{negate} * Inverse(M_{viewtoworld})$$其中,$M_{negate}$ 为因为观察空间是右手坐标系,所以需要对 Z 取反:
$$M_{negate} = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 &1
\end{pmatrix}
$$其中,$M_{viewtoworld}$ 为将物体从观察空间转化到世界坐标系的矩阵:
$$M_{viewtoworld} = \begin{pmatrix} \overrightarrow {Up}.x & \overrightarrow {Up}.y & \overrightarrow {Up}.z & 0\\ \overrightarrow {Right}.x & \overrightarrow {Right}.y & \overrightarrow {Right}.z & 0\\ \overrightarrow {Forward}.x & \overrightarrow {Forward}.y & \overrightarrow {Forward}.z & 0\\ {O_{origin}}.x & {O_{origin}}.y & {O_{origin}}.z & 0 \end{pmatrix}$$- 其中,$Inverse()$ 的功能是求一个矩阵的逆
2.1.4 裁剪空间
顶点接下来需要从观察空间转化到裁剪空间中,裁剪空间的作用是为了方便剔除渲染图元:完全在这个空间内部的图元会被保留,完全不在这个空间内部的图元会被剔除,和这个空间相交的图元会被剪裁。
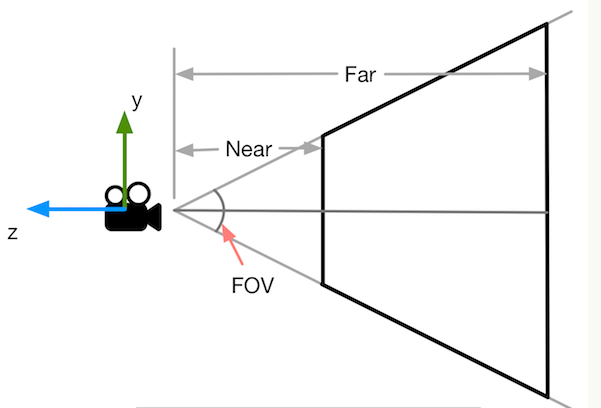
裁剪空间实际上就是一个视锥体:
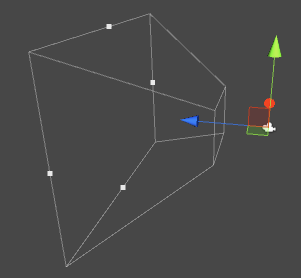
这个视锥体实际上可以由近剪裁平面距离Near、远剪裁平面距离Far、FOV、Aspect(宽高比)这几个参数决定。
将物体从观察空间转换到剪裁空间中的矩阵 $M_{frustum}$ 如下:
$$M_{frustum} = \begin{pmatrix}
\frac{cot(\frac{FOV}{2})}{Aspect} & 0 & 0 & 0\\
0 & cot(\frac{FOV}{2}) & 0 & 0\\
0 & 0 & - \frac{Far+Near}{Far-Near} & - \frac{2*Near*Far}{Far-Near} \\
0 & 0 & -1 & 0
\end{pmatrix}$$
转换公式如下:
$$P{clip} = M{frustum} * P_{view}$$
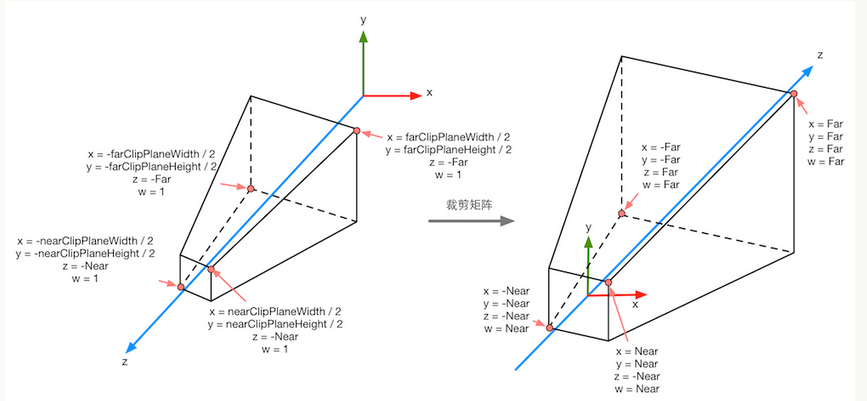
上面的左图,是在观察空间的视锥体的四个顶点。上面的右图,经过变换后的视锥体的四个顶点。由图中可以看到,这个转换实际上就是对观察空间中的点做了一次平移+缩放的变换。
2.1.5 屏幕空间
将顶点从剪裁空间变换到屏幕空间后,就可以得到这个点在屏幕上对应的像素坐标了。由于这个变换在接下来的程序中不是很重要,所以在这里就不过多讲述了。
2.2 网格投影的基本原理
2.2.1 基本概念
它的基本思想就是,将一个在剪裁空间中的,正对相机的网格,投影到世界空间中的海平面上。
其直观的算法为:
- 在剪裁空间中,创建一个正对摄像机的,正方形的网格。
- 将这个网格投影到世界空间的一个平面上。这个平面就是海平面$S_{base}$。
- 将这个世界空间中的点,根据高度图($f_{HF}$),替换为对应的点。
- 渲染这个平面。
2.2.2 一些定义
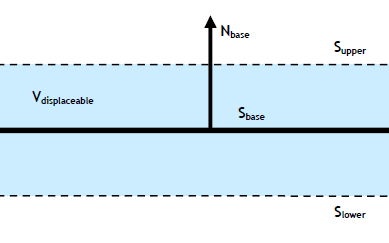
$S{base}$:世界坐标系中,被替换前的海面。这个海面上的每个点都将会被$f{HF}$替换为对应的高度。
$S_{upper}$:整个海面被替换后的最高点所在的平面。
- $S_{lower}$:整个海面被替换后的最低点所在的平面。
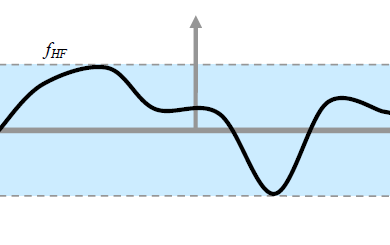
- $f{HF}$:将海面上每个点替换为对应点的函数。$f{HF} = f(x, y)$。
- $V_{displaceable}$:在最高面和最低面之间的长方体。
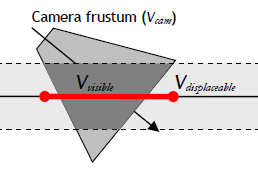
- $V_{camera}$:视锥体所形成的平截椎体。
- $V_{visible}$:视锥体可以看到的体积。其实就是视锥体与海体的相交的部分。
2.2.3 具体算法
生成投影网格的具体算法如下:
- 获得摄像机 camera 的位置和方向,以及其他必要的属性。
- 确定 $V{camera}$ 与 $V{displaceable}$ 是否有交集。如果没有交集,那么说明相机看不到海面,停止一切工作。具体算法在 2.2.3.2 节有。
- 重新计算相机 newCam 的位置和方向(这个新相机和实际的相机会有一点点不同),计算得到 newCam 的从世界空间转化到相机空间的矩阵 $M{pview}$,还有从相机空间转化到剪裁空间的矩阵 $M{pclip}$。
我们就可以得到从剪裁空间到相机空间的矩阵 $M{projector}$:
$$M{projector} = [M{pclip} * M{pview}] ^ {-1}$$ - 考虑到实际的体积 $V{visible}$ 是 $V{displaceable}$ 和 $V{camera}$ 的相交的部分,所以需要计算 $V{visible}$ 在剪裁空间中的 x 和 y 方向的扩张的部分。构造这样一个矩阵 $M{range}$,它可以将 [0, 1] 转换到这个扩张的部分。更新投影矩阵 $M{projector}$:$$M_{range} = \begin{pmatrix} \frac{xMax - xMin}{2} & 0 & 0 & xMin\\\ 0 & \frac{yMax - yMin}{2} & 0 & yMin\\\ 0 & 0 & 1 & 0 \\\ 0 & 0 & 0 & 1 \end{pmatrix}$$
$$M{projector} = M{range} [M_{pclip} M_{pview}] ^ {-1}$$
- 创建一个x、y都在 $[0, 1]$的网格。
6.将网格中的每个点,首先投影到世界空间下,视锥体的近剪裁面上,然后投影到视锥体的远剪裁面上,最终的点就是这两个点组成的线与海平面 $S_{base}$的交点。 - 将这个在 $S{base}$ 上的点,根据高度函数 $f{HF}$,替换为最终的点。