A* 寻路算法

因为要学习英语，所以我在这里就翻译翻译文章。这样既提高了我的英语水平，也可以学习一点编程方面的知识。

这次要介绍的是 A* 算法, 它包括了算法的由来、通用算法和计算过程，最后给出了在 Unity 中的实现。

原文链接：这里

简要介绍 A* 寻路算法

你想拥有一个，能让怪物或玩家移动到一个特定的点上，同时避免撞到墙和障碍物上的游戏吗？

如果你想拥有的话，读读这篇文章，我们将会向你展示你怎样用 A* 寻路算法 做到这一点！

网上已经有许多关于 A* 寻路算法 的文章了，但是它们中的大多数都是写给那些已经有经验的、懂得基本原理的开发者们的。

这篇教程采用从基本原理入手的方法来讲解。我们讲一步一步的讲解 A* 算法 是如何实现的，包含了大量的图片和例子来用图解法讲解这个过程。

不管你是用的什么编程语言，或者是什么平台，你都会发现这篇教程很有用 – 因为它以一种通用语言格式来解释算法的。

那么，现在先找到一条最短的到达含咖啡因饮料喝美味小食的路径，让我们开始吧！ :)

一只寻路的猫

让我们开始想象我们有一个这样的游戏：一只猫想要找到一条通往一根骨头的路。

“为什么世界上会有一只猫想要得到一根骨头呢？”你可能会这么想。好吧，在我们的游戏里，这是一只聪明的猫，他想捡起骨头给狗狗，去避免使它自己被狗狗们咬！ :]

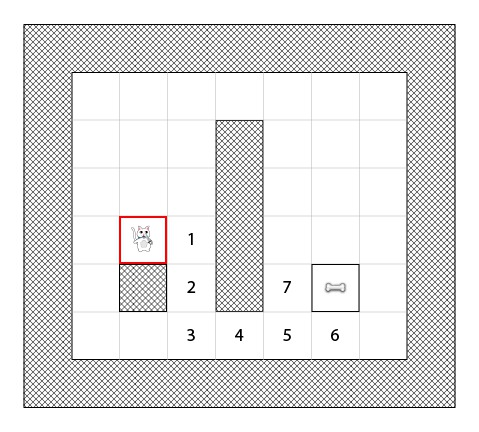
那么，让我们想象下面这张图片里的猫想要找到通往骨头的最短路径。

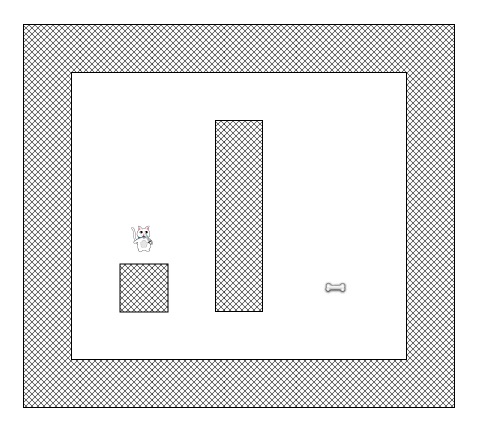
令人悲伤的是，猫咪不能直接从他目前的位置走到骨头所在的位置，因为有一面墙挡住了路，而他在游戏中也不是一个无实体的鬼魂！

我们游戏里的这只猫也很懒，所以他一般来说想要找到一条最短的路径，这样当他回家面对他的妻子的时候就不会很疲倦了。

那么现在我们怎么才能写出一个算法去找到猫咪应该走的最短路径呢？ A* 就是解救方法。

将搜索区域简单化

在寻路过程中，我们要做的第一步就是将搜索区域简化为一些我们能够很容易管理的东西。

具体怎么去做这个取决于你的游戏。例如：我们可以将搜索区域分隔成一个一个的像素，但是这个对于我们这种基于瓷砖（tile）的游戏来说，像素这个单位太小了。

所以，我们将用瓷砖（正方形）作为基本单位在寻路算法中使用。其他形状的也可以（例如三角形或六边形），但是正方形是最符合我们需要的，而且也是最简单的。

像这样分隔开来，我们的搜索区域就可以被简单的表示为一个二维数组。所以当我们的关卡有 25x25 的瓷砖时，我们的搜索区域就是一个有着625个正方形的数组。如果我们将我们的地图以像素分隔开来时，我们的搜索区域就将会是一个有着 6400,000 个正方形的数组（一个瓷砖有 32x32 个像素）！

开放表和闭合表

现在我们已经建立一个简单的搜索区域，让我们来讨论 A* 算法 是怎么实现的。

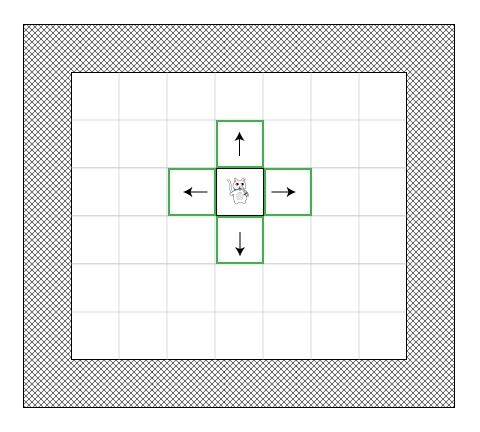
我们的猫咪除了懒惰，记性也不好，所以他将需要两个表：

1. 一个表用于记录所有正在被考虑、用于找到最短路径的方格（我们叫它开放表）
2. 一个表用于记录所有不需要被再次考虑的方格（我们叫它闭合表）

刚开始时，猫咪将他目前的位置（我们将称呼这个开始的点为点“A”）加入闭合表中。然后，他将所有邻近他的、可以行走的方格加入开放表中。

这儿有一个例子展示了如果猫咪站在一个开放位置，应该怎么做（绿色代表开放表）

路径代价

我们将给每一个方格一个分数：G + H

• G 代表着从开始点“A”到目前所在方格的代价。所以，对于一个邻近开始点“A”的点来说，代价就是1, 但是当我们离开始点越远时，代价就会增加。
• H 代表着从当前点到目的地点的预计代价（我们将把骨头所在的点称为点“B”）。这个代价通常是尝试性的计算得出的 – 因为我们不知道真正的代价是多少，这仅仅是一个估计。

你可能会想，“移动代价”的含义是什么。其实在游戏中这个相当简单 – 仅仅只是方格的数量罢了。

然而，记住在我们的游戏中，你可以赋予它不同的含义。例如：

• 如果你允许对角线移动的话，你可能会将对角线移动的代价设置得略高一点。
• 如果你有几种不同的地形，你可能会设置不同的移动代价在不同的地形上。

这就是大致的想法 – 现在让我们深入来更具体的计算 G 和 H 吧。

关于 G

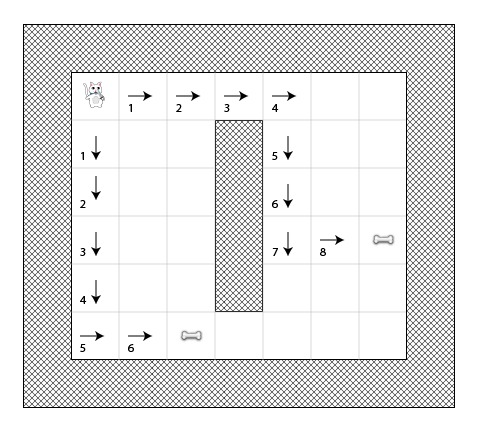
为了计算 G，我们需要将上一个 G （我们来的那个方格）再加上1。因此，每一个方格的 G 值将代表从 A 点沿路径到这个方格的总代价。

例如，下面的图表展示了两条到不同骨头的路径，每一个方格的 G 值都已经标记上去了。

关于 H

回忆一下：H 是从当前方格到目的地的预计花费。

预计花费越接近实际代价，最终的路径就会越准确。如果预计得不够准确，那么生成的路径可能不是最短的（但是它可能会很接近）。这个问题太过于复杂以至于我们将不会在这篇教程中讨论它，但是我还是会在文章末尾给予你一个将它解释得十分详尽的链接。

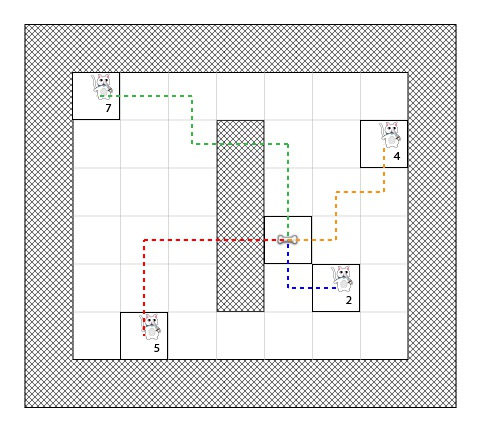
为了将它简单化，我们将会用到“曼哈端距离算法”（译注：Manhattan distance method），这个算法仅仅只是计算了当前点到 B 点的水平方向和竖直方向上的方格数，而没有将障碍物或不同地形考虑进来。

例如，下面用图表展示了在不同起始点下，用“曼哈端距离算法”模拟的 H 值（显示在黑框中）

A* 算法

那么现在你知道了如何去计算每一个方格的分数（我们将把这个叫做 F，它等于 G + H）

猫咪会重复一下步骤来找到最短路径：

• 在开放表中拿到一个分数最低的方格，我们将这个方格叫做方格 S
• 在开放表中移除方格 S，然后将 S 放入闭合表中
• 对于在方格 S 的每一个相邻的方格 T
  • A. 如果 T 在闭合表中：忽略它
  • B. 如果 T 不在开放表中：将它加入开放表中，然后计算它的代价
  • C. 如果 T 已经在开放表中：检查如果我们用当前生成的路径到达终点的话，F 值会不会更低。如果是的话，那么更新它的数值，然后也更新它的父节点

如果你对它还不太了解的话，别担心 – 我们将通过一个简单的例子来一步一步的演示它是怎样工作的！ :)

猫咪的路径

让我们以一个懒猫如何找到骨头的作为例子。

在下面的表格中，我已经根据如下的方式列出了 F = G + H 的值:

• F（每个方格的数值）： 最左上角
• G（从 A 到当前方格的代价）： 左下角
• H（从当前方格到 B 点的预估代价）： 右下角

除此之外，箭头表示了到达该方格的移动方向。

最后，每一步的红色方格代表闭合表，绿色方格代表开放表。

好，让我们开始吧！

Step 1

在第一步，猫咪确定了在离他开始点（点 A）相邻的可行走的方格，计算它们的 F 值，然后将它们加入它的开放表中。

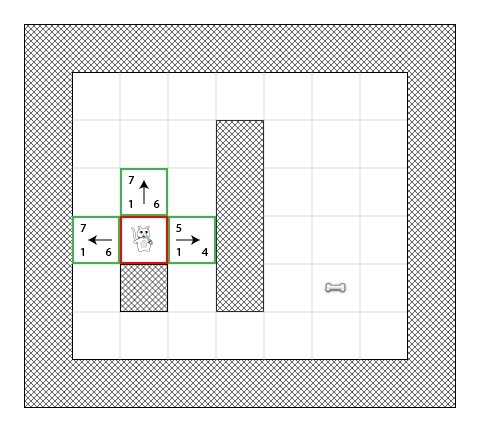
你会发现每个方格的 H 值都已经列出来了（其中两个是6，一个是4）。我建议你以 “曼哈瑞距离算法”来计算每一个方格的 H 值，以便于你理解。

同样需要提醒的，F 值（在左上角）就仅仅是 G+H 的值。

Step 2

在下一步，猫咪选择了 F 值最低的方格，将它加入闭合表中，然后检索它的邻近方格。

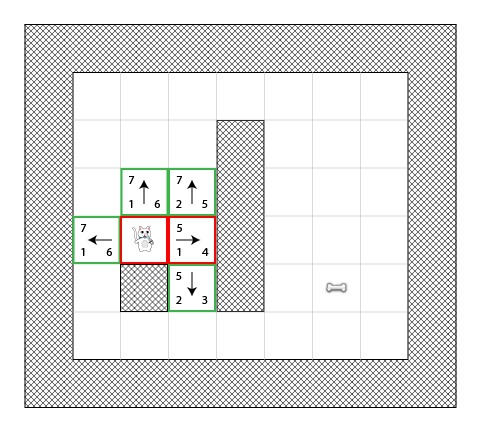
在这里你能看到，代价最低的方格是 F 值为 5 的方格。它尝试将所有的相邻方格加入开放表中（然后计算它们的数值），要注意到它不能将猫咪所在的方格加入开放表（因为他已经在闭合表中了），那些障碍物方格也不能加入（因为它是不可行走的）。

需要注意的是：对与两个新加入开放表的方格，它们的 G 值已经加了一，因为它们离初始点有两个方格的距离。你同样也需要用“曼哈瑞距离算法”来确定每个新方格的 H 值。

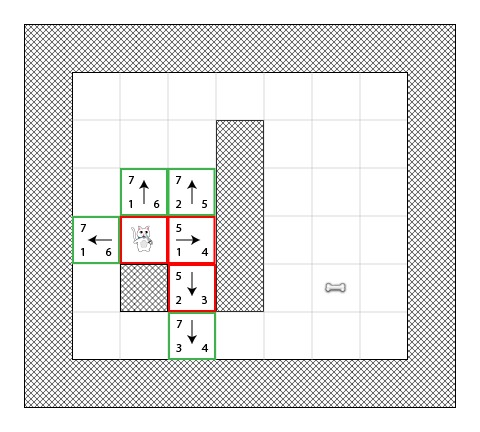
Step 3

同样的，我们选择了有着最低 F 值的方块，然后继续迭代：

Step 4

在这里我们有一个有趣的例子。在上一张图片中你可以看到，现在有 4 个方块有着相同的 F 值为 7 — 我们现在应该怎么做？

这里我们有几种方式可以用，但是一个简单的（也是快速的）方式是继续跟着最近一个加入到开放表中的方格。所以我们继续跟着最近一个刚刚加入带开放表中的方格：

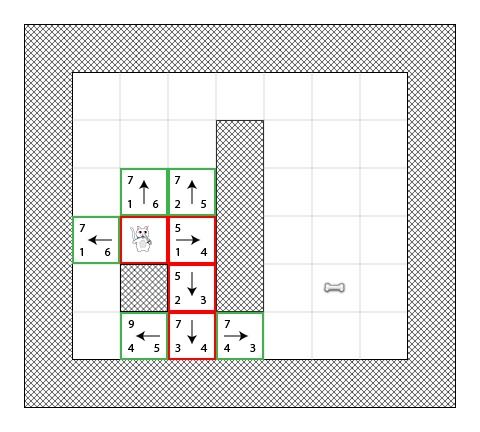
这一次有两个相邻的而且可以行走的方格，我们像以前那样计算它们的分数。

Step 5

像往常一样，我们选择了有着最低分的方格（7），而且为了保持一致我们这次选择了最邻近的一个方格。

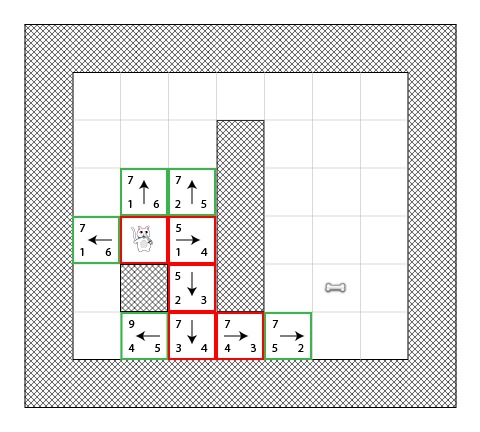
这一次只有一种可能性，我们越来越接近了！

Step 6

你现在越走越近了！我敢打赌，你会猜测下一步是这样子的：

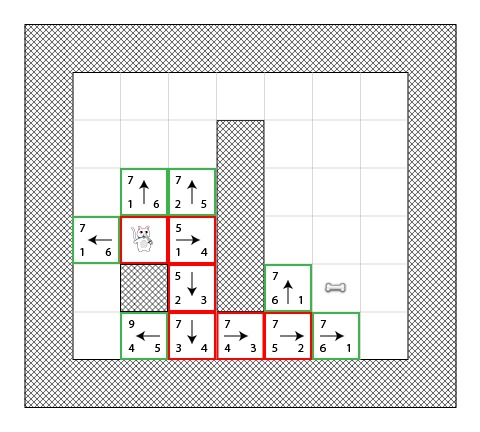
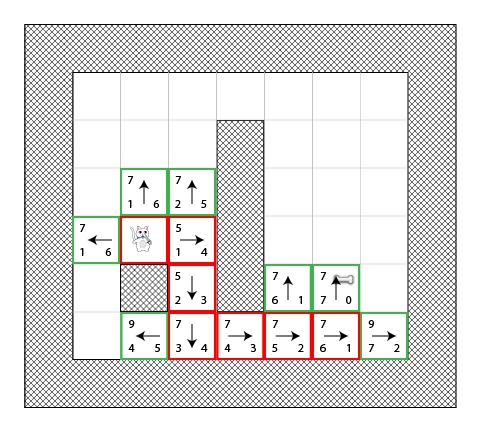
我们几乎就要到了，但是这次，你可以看见，现在这里我们有两条最短的路径达到目的地，我们可以在这两者之间选择。

在我们这个例子中，有两条最短路径：

• 1-2-3-4-5-6
• 1-2-3-4-5-7

在真正的代码实现中，我们选择哪条路并不重要。

Step 7

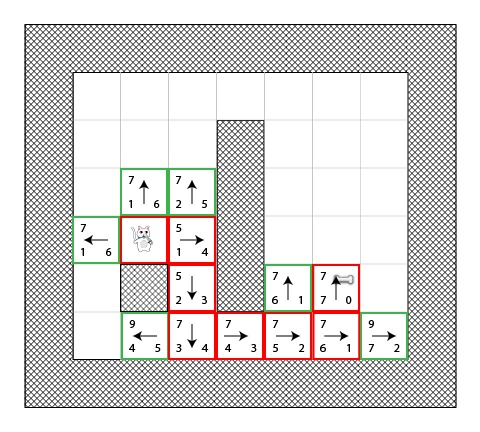
让我们再次迭代这些方格：

啊哈，骨头现在在开放表中！

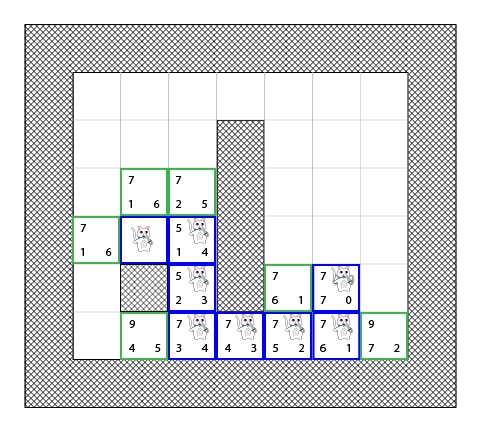
Step 8

当我们的目标在开放表中时，算法会将它加入到闭合表中：

然后，算法所有需要做的就是返回去，找到最终的路径。

一个没有眼光的猫咪（A Non-Visionary Cat）

在上面这个例子中，我们可以看到，当猫咪在寻找最短路径时，它通常会选择最优的方格（在它的未来是最短路径的上的方格） – 看起来它是一个有眼力的猫咪！（译注：指的应该是贪心的意思）

但是，当我们的猫咪，没有那么聪明，而且总是选择开放表中 F 最低的方格加入它的闭合表会怎么样呢？

下图展示了所有在寻找最短路径的过程中所需要的所有方格。你可以看到：猫咪尝试了更多方格，但是它仍然找到了最短路径（和之前展示的不是一样的，但是另一种相等）：

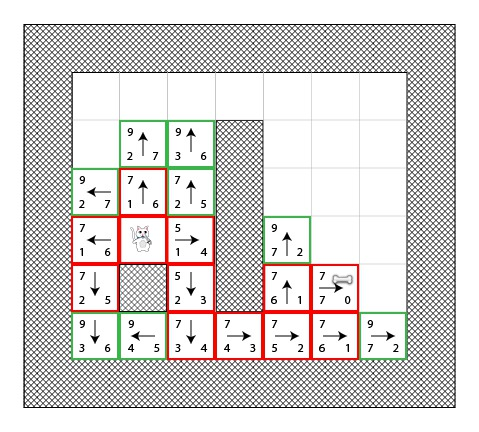
在图中，红色方格并不代表最短路径，它们仅仅只是表示它们在有些时候被选为了 “S” 方格。

我建议你看看上面的表格，然后尝试自己走走它。这一次，无论何时你看到了一个分数平等的方格，你就去选择它。你会发现你最后仍然会以最短路径结尾。

所以，你会发现，跟着 “错误” 的方块走也没有问题，你仍然会以最短路径结尾，即使它可能会让你多迭代几次。

所以在我们的实现中，我们将以以下算法将方格加入到开放表中：

• 相邻方格将会以这样的顺序返回：上/左/下/右
• 一个方格将会被添加入开放表中，在所有有着相同代价的方格之后（所以第一个加入开放表中的方格将会是第一个被猫咪选择的方格）

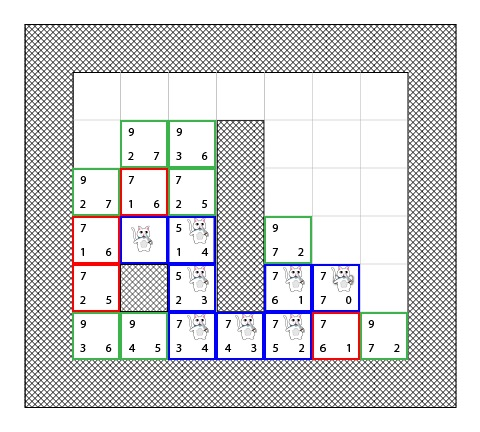
下面是一个用图表展示的回溯过程：

下面是用伪码实现的算法，其实它是用 Object-C 写的，但其实它可以用任何语言实现。

[openList add:originalSquare]; // start by adding the original position to the open list
do {
	currentSquare = [openList squareWithLowestFScore]; // Get the square with the lowest F score
	
	[closedList add:currentSquare]; // add the current square to the closed list
	[openList remove:currentSquare]; // remove it to the open list
	
	if ([closedList contains:destinationSquare]) { // if we added the destination to the closed list, we've found a path
		// PATH FOUND
		break; // break the loop
	}
	
	adjacentSquares = [currentSquare walkableAdjacentSquares]; // Retrieve all its walkable adjacent squares
	
	foreach (aSquare in adjacentSquares) {
		
		if ([closedList contains:aSquare]) { // if this adjacent square is already in the closed list ignore it
			continue; // Go to the next adjacent square
		}
		
		if (![openList contains:aSquare]) { // if its not in the open list
			
			// compute its score, set the parent
			[openList add:aSquare]; // and add it to the open list
			
		} else { // if its already in the open list
			
			// test if using the current G score make the aSquare F score lower, if yes update the parent because it means its a better path
			
		}
	}
	
} while(![openList isEmpty]); // Continue until there is no more available square in the open list (which means there is no path)

接下来要做的

恭喜，你已经知道了 A* 算法的基本原理！

如果你想知道关于 A* 算法的更多的东西的话，你可以看看这里：Amit’s A* Pages